[에라둔] 역학 문항에서의 미래와 과거
계산적으로 중요한 내용들은 아니고 그냥 편히 읽으시면 될법한 내용들입니다.
역학 문항을 풀다 보면 여러가지 상황을 마주하게 되는데
종종 동일한 카테고리를 마주하게 됩니다.
이번에 다룰 내용은 어찌보면은 상대속도와 조금 관련이 있을 수 있습니다만 일단 접어두고.
아래 문항들의 공통점이 무엇일까요?

20230618


20210911


20130920
세 문항의 공통점은 두 물체가 모든 지점에 대하여 운동 방향, 속력 모든것이 동일한 상황들입니다.
이전에 저도 문항 출제를 할 때 위와 같은 상황을 이용하여 문항 출제롤 하곤 했는데
위와 같은 문항을 출제하면 참 좋은게 v-t그래프를 옆으로만 삭 밀어주면 되기 때문에
검토하기가 수월해서 즐겨냈었던 기억이 어렴풋이 납니다.
거두절미하고
어떻게 보면 위와 같은 문항들은 상대속도를 활용할만한 문항들 중에서도 특수한 케이스라고 생각을 하는데
저같은 경우에는 두 물체에 대하여 가상의 시간차 t를 가정하고 문제 풀이를 하는것을 선호합니다.
뿐만 아니라, 시간차 t가 난다고 생각하고 문항을 바라보면 좀더 문제 상황을 직관적으로 파악하기도 좋지요.


예를 들어 위 문항의 경우엔 B의 2초 뒤 모습이 A라고 생각하면서 풀면 문제 풀이가 아마 수월하겠죠.
일단 ㄱ이 바로 나올것이며
2초뒤 B가 정지할테니 평균속력 2라는 점에서 v=4가 바로 나올것이며
dv=4인동안의 시간이 2초니 가속도가 2인것도 술술 나올것입니다.


20210911
마찬가지로 위 문항도 B가 t초뒤의 A모습이라고 가정한다면 3vt=L이 나올것이며
우리는 자연스레 A가 p에서 q까지 이동하는데 걸리는 시간이 t라고 할것이기에
평균 속력 공식을 이용하여 1.5vt=0.5L과 같이 문항들이 순둥순둥하게 풀릴것입니다.
위와같이 동일한 경로, 운동 상황을 공유하는 문항의 경우에는 결국엔 대부분 문항에서 요구하는것은
두 상황에 대한 연립일것이며, 이 연립과정이 가감의 과정이기 떄문에
사실 t로 두고 문항을 풀면 쉽게 풀리는 경우가 많습니다.


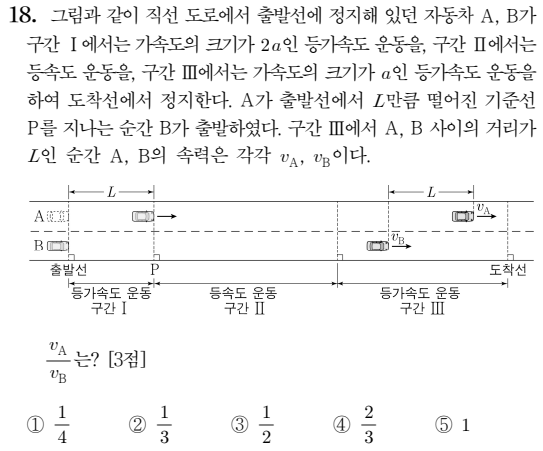
20230618
위 문항의 경우에도 마찬가지로 역시 B의 t후 모습이 A라 생각하고 풀면 풀기가 수월할것입니다.
등가속도 운동 구간 I에서의 가속도를 2a라 하면 (0+2at)t/2=att=L이 나올것이며
이후 vb인 B가 시간 t 후 속력이 va가 된다고 하면 자연스레 (va+vb)/2 * t = L이 나오게 될것입니다.
그리고 구간 3에서 시간 t동안 속력이 변하였는데 이것이 va-vb일지 vb-va일지는 잘 모르겠습니다.
사실 시간 t라는 차이를 생각해보면 B가 출발할 때 이미 가속된 A가 있기에 거리차가 L보다 벌어질텐데
다시 L로 감소했다는 포인트를 보면 아마 가속도가 감소했음을 알기 수월하겠지요.
그러한 이유로 (va+vb)=2L/t, (vb-va)=at=L/t
va+vb : vb-va = 2:1, 2vb-2va = va+vb, 3va=vb, va:vb=1:3 이 나오게 될것입니다.
저같은 경우에는 두 물체가 동일한 경로를 운동하면 습관적으로 동일한 운동까지 하는지를 체크합니다.
아마 위와같은 유형들을 깔끔하게 푸시는 분들이라면 위의 개념을 숙지한 상태에서
그 이상은 본인의 직관, 암산 등으로 인한 최적화 정도의 차이만이 존재할것입니다.
만약, 위와 같은 수식적 풀이가 다소 어렵다면 그냥 모든 시간 영역을 t미지수로 두고 풀어보시거나
vt 그래프를 정성스럽게 그려보시는것을 권장드립니다.
아마 그래프를 그리시다 보면 자연스레 평행사변형과 친해지게 될겁니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
잘자라 7
잘 때는 단세포처럼
-
작수 25555 지방 사립대나 지거국 완전 최하위과 가능했네요 수능 생각보다는...
-
시대재종 합격 뱃지 10
있으면 개 웃길듯ㅋㅋ 그냥 써봄..
-
앙 2
기모찌
-
아 진짜자야한다 2
안녕히 주무시고 내일도 좋은 하루 보내세요 우리는 모두 소중한 사람임
-
다해줬잖아 0
(수학 4등급을 쳐맞고 사탐을 갈아마시며)
-
문과 기준임 ㅇㅇ 영어 반영비도 많이 줄었고(16.7>12.5) 사탐가산이 교차표본...
-
이미지 써주면 맞이미지 13
-
의대 이월 늘어나면 연쇄적으로 입결에 영향이 갈텐데 이거 정시러들한테 좋은거...
-
ㄱㄱ
-
분명 스캠이 맞긴 맞는데 버블이 터지지 않고 계속 유지되는 스캠 나까지만 어떻게 잘...
-
굿밤 0
내일 오전 8시에 약속인데
-
우리집에 가면 12
책-상도 있고, 연-필도 있고 암튼 이 노래 아시는분 계신가요
-
ㅇㅈ메타해주세요 0
잘생기면 쪽지할게요
-
그렇게 올리면 딱히 모르거나 호감이어도 비호감 누름
-
게임시작할때 "저 마이크돼요" 한마디만해줘도 사기충전MAX되는데 마이크되면...
-
저렇게 텅텅이라니 하긴 원서 한장인데 반영비 맞는 고대쓰는게 맞긴함 ㄹㅇ로 1번 더...
-
다소 어둡지만•• 저는 강박증, 불안장애, 약한 공황을 4년째 앓고 있습니다 1년...
-
비뇨기과 가면 처방받고 주사 맞을 수 있나?
-
얼버기 3
-
ㅇㅋ 휴릅함 6
오늘 오후에 다시 돌아옴뇨 그리고 다들 좋은 밤 되세요!
-
다른 유빈씨가 유명해져서..
-
무네가 가슴이잖아요 옵빠이가 좀 천박하게 말하는건가요 둘의 차이 아시는분?
-
안녕하세요. 저는 이번에 경희대 한약학과에 수시로 입학하게 된 학생입니다. 다름이...
-
궁금하다
-
여기 진짜 가고싶은데… 갑자기 2칸이 떨어지네..
-
도저히 문돌이가 되지는 못하겠다
-
4분 계시던데 각 선생님 특징과 왜 추천하는지 물어볼 수 있을까요?
-
호불호조사 0
.
-
얼박사 만들어먹으면 깸..왜지
-
. 1
..
-
그래그래 그건 사실이야
-
컴공 일기260 5
https://www.acmicpc.net/problem/6236 백준 6236번...
-
알려주시면 감사하겠습니다.
-
비호감 2명 누구냐 14
자수하셈
-
ㅇㅈ 6
앗 정상화의 신이
-
학생동 1순위 선발 기준에 전형별/모집단위별 입학 순위를 고려하는데 만약에 제가...
-
장원영 레전드 6
연말에 인생샷이 나올줄은
-
내신 2점 후반대~3점 초반대까지는 써볼만한거 아님? 몇몇과들은 거의 정시일반이랑...
-
ㄱㄱ
-
내가 미친 루팡이었네
-
갑자기 이상한 영어로기쿠키가 없다면서 안들와졌는데 보고싶었어
-
재수 여파로 4
고3인데 생기부 써야하는 내 인생 ㄹㅈㄷ
-
욕먹을까봐 못올리겠음 ㅇㅇ
-
자라 이것들아 3
2시 넘었어
-
쫄린달까
-
ㅠㅠㅠㅠㅠ

















































옆동네 옆옆동네에서 잘 보고 있습니다감사합니다!!
와 쌤 과외 받았던 학생인데,,, 잘 계시나요 ㅠㅠ
감사했습니다!! 덕분에 카이스트 가서 잘 지내고있어요